Le theoreme de Thales est un des deux théorèmes les plus importants, qui sont vus au collège.
Avec sa réciproque et le théorème de la droite des milieux, il est indispensable de bien le comprendre et de le maîtriser pour obtenir une bonne note en mathématiques au brevet…
Sur cette page, nous proposons de t’expliquer :
- Premièrement, quand peux-tu utiliser le theoreme de Thales ?
- Deuxièmement, uelle est sa définition et à quoi il va te servir ?
- Troisièmement, que sont la réciproque de Thalès et le théorème de la droite des milieux ? et à quoi ils te seront utiles ?
Enfin, nous mettons gratuitement à ta disposition 5 exercices corrigés pour t’entraîner et réviser à la maison.
Quand peux-tu utiliser le theoreme de Thales ?
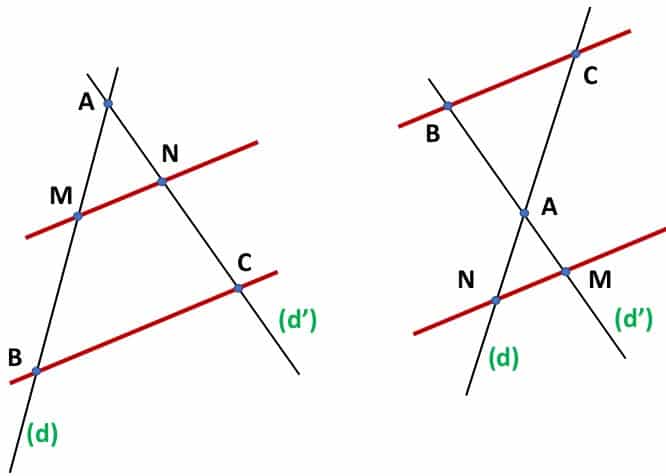
La première chose à savoir est que le théorème de Thalès s’applique lorsque l’on a :
- deux droites sécantes (d) et (d’) sécantes ;
- deux droites parallèles et distinctes qui ne passent pas par le point d’intersection de(d) et (d’).
Pour faciliter l’explication du theoreme de Thales, on retiendra les deux configurations suivantes :
Définition du theoreme de Thales
Voici l’énoncé du theoreme de Thales et le raisonnement que tu dois apprendre par cœur pour les utiliser dans tes exercices de math :
Caractéristiques connues :
- Soit (d) et (d’) deux droites sécantes en A.
- B et M sont 2 points appartenants à la droite (d), distincts de A.
- C et N sont 2 points de la droite (d’), distincts de A.
- Les droites (BC) et (MN) sont parallèles.
Théorème et conclusion :
D’après ces caractéristiques, on peut écrire grâce au theoreme de Thales que :
\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}
Nota : Bien évidemment, tu devras adapter le nom des points, des segments et des droites selon les caractéristiques de ton exercice de math.
Astuce pour écrire les égalités du théorème de Thalès
Le theoreme de Thales nous a permis d’écrire les deux égalités suivantes :
\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}
Mais attention, il ne faut pas faire d’erreur en inversant les points…
Voici notre méthode pour écrire ces égalités sans se tromper :
- Tu dois repérer le point d’intersection (ici nommé A) des deux droites non-parallèles (d) et (d’) ;
- Tu choisis l’une des deux droites (d) ou (d’), qui passe par le point d’intersection.
Par exemple, on choisit la droite (d) sur laquelle se trouve les points A, M et B ;
- En partant du point d’intersection (A), tu écris le rapport de la longueur plus petit segment [AM] par la longueur du plus grand segment [AB] ;
- Puis tu fais la même chose sur l’autre droite ;
5. Pour les droites parallèles, on écrit le rapport du plus petit segment [MN] par le plus grand [BC].
Définition du theoreme reciproque de Thales
Le théorème réciproque de Thalès te permettra de prouver que des droites sont parallèles ou pas.
Voici son énoncé et le raisonnement que tu devras écrire dans tes exercices de géométrie :
Caractéristiques connues :
- Soit (d) et (d’) deux droites sécantes en A.
- B et M sont 2 points de la droite (d), distincts de A.
- C et N sont 2 points de la droite (d’), distincts de A.
- Si \frac{AM}{AB}=\frac{AN}{AC} et les points A,M,B sont alignés dans le même ordre que les points A,N,C, alors on peut utiliser le théorème suivant :
Théorème et conclusion :
D’après le théorème réciproque de Thalès, on peut affirmer que les droites (MN) et (BC) sont parallèles.
Nota : N’oublie surtout pas de vérifier l’alignement des points dans le bon ordre, sinon ta démonstration sera considérée comme fausse par ton professeur.
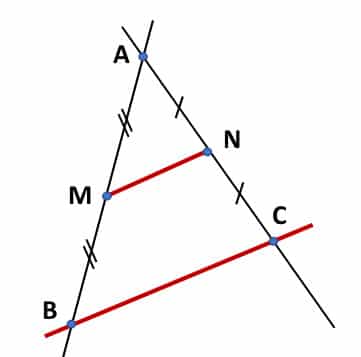
Définition du théorème de la droite des milieux
Énoncé du théorème de la droite des milieux à citer dans ton raisonnement :
« Dans un triangle, lorsqu’un segment joint les milieux de deux des côtés, alors il est parallèle au troisième côté, et sa longueur est égale à la moitié de la longueur de ce côté« .
Le théorème de la droite des milieux peut être illustré avec la figure géométrique suivante :
A quoi sert le theoreme de Thales et sa réciproque ?
Dans de nombreux problèmes de géométrie au lycée comme au collège, le theoreme de Thales est la solution car il permet de démontrer beaucoup de choses.
Par exemple, tu pourras :
- D’abord, calculer les longueurs de segments de droite ou des cotés d’un triangle ;
- Ensuite, démontrer que des droites sont parallèles ;
- Puis, prouver que des droites sont sécantes en un point ;
- Ou encore démontrer que des points sont alignés dans un ordre précis.
Dans ce qui suit, nous présentons un récapitulatif et des exemples détaillés montrant l’utilité des 3 théorèmes que nous avons vus.
Exemple 1 : calcul des longueurs grâce au theoreme de Thales
Énoncé :
Dans la figure ci-dessous, les droites (d) et (d’) sont sécantes en A, les droites (BC) et (MN) sont parallèles, et on connait les distances suivantes :
AM = 7,2 cm, AB = 10,8 cm, AN = 6 cm et BC = 5,1 cm .
Question : Calculer les longueurs des segments MN et AC ?
SOLUTION
Caractéristiques connues :
- Tout d’abord, on sait que les droites (d) et (d’) sont sécantes en A.
- Ensuite, on sait que B et M sont 2 points appartenants à la droite (d), distincts de A.
- Puis, que C et N sont 2 points de la droite (d’), distincts de A.
- Enfin, l’énoncé nous indique que les droites (BC) et (MN) sont parallèles.
Theoreme de Thales et conclusion :
D’après ces caractéristiques, on peut écrire grâce au théorème de Thalès que :
\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}
d’où :
\frac{7.2}{10.8}=\frac{6}{AC}=\frac{MN}{5.1}
On déduit alors que :
7.2*AC=10.8*6
10.8*MN=7.2*5.1
donc les longueurs AC et MN sont égales à :
AC = \frac{10.8*6}{7.2} = 9 cm
MN = \frac{7.2*5.1}{10.8} = 3.4 cm
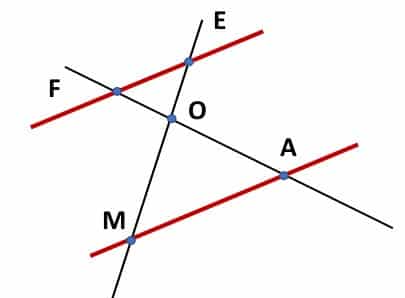
Exemple 2 : Prouver que des droites sont parallèles grâce à la réciproque de Thalès
Énoncé :
OF = 2,4 cm, OE = 3 cm, OM = 3,5 cm et OA = 2,8 cm.
Question : Prouver que les droites (MA) et (FE)sont parallèles ?
SOLUTION
Caractéristiques connues :
Pour démontrer le parallélisme entre les deux droites MA et FE, c’est très simple. En effet, nous pouvons nous intéresser au rapport de proportionnalité existant entre les longueurs, qui nous sont données.
Ainsi, il suffit de procéder au calcul des quotients suivants :
\frac{OE}{OM}=\frac{3}{3.5}= 0.857
\frac{OF}{OA}=\frac{2.4}{2.8}= 0.857
On a donc l’égalité suivante :
\frac{OE}{OM}=\frac{OF}{OA}
Théorème de Thales et conclusion :
Comme les points M, O et E d’une part, et les points A, O et F d’autre part sont alignés dans le même ordre, alors d’après le théorème réciproque de Thalès, on peut affirmer que les droites (MA) et (FE) sont parallèles.
Notre article sur le theoreme de Thales t a plu, alors n’hésite pas à le partager sur les réseaux sociaux.