Au collège, le théorème de Pythagore est l’une des notions les plus importantes en mathématiques, tout comme le théorème de Thalès !
Il est au programme de quatrième et tu le retrouveras certainement au brevet des collèges…
Ainsi, il est essentiel de le comprendre et de savoir l’utiliser parfaitement pour résoudre tous les problèmes.
Dans cet article, nous te proposons donc d’apprendre :
- Quelle est la définition du théorème de Pythagore et à quoi il sert ?
- Quand et comment l’utiliser pour résoudre les problèmes de géométrie ?
- Qu’est ce que la réciproque du théorème de Pythagore et à quoi elle sert ?
Enfin, nous t’expliquerons deux méthodes à suivre pour utiliser Pythagore et sa réciproque.
Avant de comprendre le théorème de Pythagore
La première chose à savoir est que le théorème de Pythagore ne s’applique que pour les triangles rectangles.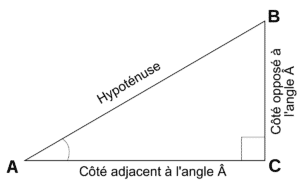
- Un triangle est dit « rectangle » s’il possède un angle droit, c’est à dire que sa mesure est égale à 90° ;
- Les deux côtés adjacents à cet angle sont appelés cathètes ou plus communément cotés adjacents.
- Le coté qui se trouve en face de l’angle droit est appelé hypoténuse ;
- Un triangle ABC est dit rectangle en C, si son angle droit se trouve au niveau du point C.
Définition du théorème de Pythagore
Le théorème de Pythagore est un théorème de géométrie qui établit une relation mathématiques simple entre les longueurs des trois côtés d’un triangle rectangle.
Son énoncé le plus connu est le suivant :
« Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. »
En nommant les sommets du triangle, le théorème s’apprend de la façon suivante.
Pour un triangle ABC rectangle en C, alors on peut dire que :
AC² + BC² = AB²
Avec les notations usuelles AB = c, AC = b et BC = a, la formule s’écrit :
a² + b² = c²
A quoi sert le théorème de Pythagore ?
Dans les problèmes de géométrie au collège, le théorème de Pythagore est souvent la clé car il permet de calculer et de démontrer de nombreuses propriétés pour les triangles.
Voici un récapitulatif et des exemples précis de ce qu’il permet de faire :
Application du théorème de Pythagore : calculer la longueur de l’hypoténuse
AB² = BC² + AC² donc AB = √(BC² + AC²)
on peut aussi écrire ces égalités sous la forme suivante :
AB² = a² + b² donc AB = √(a² + b²)
Application du théorème de Pythagore : calculer la longueur d’un côté de l’angle droit
AB² = BC² + AC²
donc BC² = AB² – AC²
on en déduit BC = √(AB² – AC²)
Application du théorème de Pythagore : prouver qu’un triangle est rectangle
Pour savoir si un triangle est rectangle, on utilise ce que l’on appelle la réciproque du théorème de Pythagore.
Souviens toi, dans le théorème de Pythagore on partait du fait que le triangle est rectangle pour arriver à calculer la longueur de ses cotés.
Avec la réciproque du théorème de Pythagore, on va partir des longueurs du triangle pour prouver qu’il est rectangle.
En effet, la réciproque s’énonce de la façon suivante :
« Si dans un triangle, le carré du plus long côté est égal à la somme des carrés des deux autres côtés, alors on peut affirmer que ce triangle est un triangle rectangle et que son hypoténuse correspond au plus grand côté ».
Par exemple :
Dans le triangle ABC, si l’on connait les longueurs AB, BC et AC et que AB est la plus grande longueur, alors il faut vérifier que AB² est égal à BC² + AC².
Si cette égalité est juste, alors cela signifie que le triangle est rectangle en C et que son hypoténuse est le coté AB !
Comment prouver qu’un triangle n’est pas rectangle ?
Puisqu’on peut prouver qu’un triangle est rectangle alors on peut logiquement démontrer qu’il ne l’est pas…
En effet, « si dans un triangle, le carré du plus long côté est différent de la somme des carrés des deux autres côtés, alors cela signifie que le triangle n’est pas un triangle rectangle. »
Autrement dit, si AB est le côté le plus long et que AB² ≠ AC² +BC² , alors on peut affirmer que le triangle ABC n’est pas un triangle rectangle.
Méthode pour utiliser le théorème de Pythagore
Dans ce chapitre, nous allons te donner une méthode précise à suivre, étape par étape, pour les exercices de géométrie, où tu dois calculer une des longueurs d’un triangle rectangle.
Avant de commencer, il faut savoir que les exercices où il faut utiliser le théorème de Pythagore sont souvent écrits de la façon suivante :
Le triangle ABC est rectangle en A et on connait la valeur de deux de ses cotés : AB et BC ou AB et AC ou AC et BC.
Et généralement, on demande de calculer la longueur inconnue du troisième côté.
Voici la méthode à suivre en 6 étapes pour trouver la réponse à ce type de problème :
Etape N°1 : identifier le coté qui correspond à l’hypoténuse
Dans l’énoncé que nous avons rédigé, il y a des données essentielles qu’il faut remarquer :
- Tout d’abord, nous connaissons la valeur de deux longueurs du triangle. Celles-ci vont te permettre de calculer la formule de Pythagore.
- Mais il y a aussi la désignation de l’angle droit du triangle. En l’occurrence il s’agit de l’angle A dans notre exemple.
En effet, comme le triangle ABC soit rectangle en A, alors cela signifie que le côté opposé à cet angle est l’hypoténuse du triangle rectangle.
Dans notre exemple, il s’agit donc du côté BC, qui est formé par les deux autres points du triangle.
Etape N°2 : calculer le théorème de Pythagore
Comme on a identifié le côté correspondant à l’hypoténuse, il nous est donc possible d’écrire convenablement la formule de Pythagore.
Pour rappel, cette formule s’écrit de la façon suivante :
« Le carré de l’hypoténuse est égal à la somme des carrés des deux autres cotés ».
Dans notre exemple, l’hypoténuse étant le côté BC, alors on peut écrire que BC² = AB² + AC²
Etape N°3 : remplacer les éléments de la formule de Pythagore par les longueurs que l’on connait
Selon les données de ton exercice, tu vas pouvoir remplacer les termes AB², BC² et AC² dans notre égalité.
Par exemple, si AB est égal à 4 cm et BC est égal à 7 cm, cela donne alors : 4²+AC²=7².
Etape N°4 : calculer le carré de ces nombres
On calcule les carrés de ces nombres, et on obtient dans notre exemple : 16+AC²=49.
Etape N°5 : isoler la longueur inconnue
En utilisant les règles sur les équations, on peut isoler la longueur inconnue d’un côté du triangle.
Dans notre exemple, on passe le nombre 16 à droite, ce qui donne AC² = 49 – 16 = 33.
Etape N°6 : calculer la racine carrée
Pour connaitre la longueur du côté inconnu, on calcule la racine carré de l’égalité précédente de tête ou avec une calculatrice.
Cela donne donc la longueur du coté AC = 5.74 cm.
Nous te conseillons d’apprendre les 6 étapes que nous t’avons expliquées pour résoudre les problèmes où il faut calculer une des 3 longueurs d’un triangle rectangle.
Méthode pour utiliser la réciproque du théorème de Pythagore
A présent, nous allons de donner une méthode à suivre pour les exercices de géométrie, où tu dois prouver qu’un triangle est rectangle.
Avant de commencer, il faut savoir que les exercices où il faut utiliser la réciproque de Pythagore sont souvent écrits de la façon suivante :
Soit ABC un triangle dont on connait les longueurs des trois cotés AB, BC et AC.
Le triangle ABC est-il rectangle ? Si oui, quel est son angle droit ?
Voici la méthode à suivre en 4 étapes pour trouver la réponse à ce type de problème :
Etape N°1 : identifier le côté le plus grand du triangle
Dans l’énoncé que nous avons rédigé, il y a trois données essentielles qui vont t’aider.
Ce sont les longueurs de chaque côté.
Si on imagine que le triangle ABC est rectangle, alors on sait que le côté opposé à son angle droit, appelé hypoténuse, est le plus grand des côtés.
Comme on connait la valeur de chaque longueur, il suffit alors de baser notre raisonnement en identifiant d’abord le côté le plus long, qui pourrait être l’hypoténuse de notre triangle.
Imaginons que notre triangle a les longueurs suivantes :
AB = 6 cm, AC = 8cm et BC = 10cm.
Ici, BC est le plus grand des côtés, donc nous allons vérifier s’il est vraiment l’hypoténuse de ABC grâce à la réciproque de Pythagore.
Etape N°2 : calculer le théorème réciproque de Pythagore
La réciproque du théorème de Pythagore dit que :
« si dans un triangle, le carré du côté le plus long est pas égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle dont l’angle droit est opposé au côté le plus long . »
Comme on a identifié le côté le plus long, il faut donc regarder si le carré de cette longueur est égale ou non à la somme des carrés des deux autres cotés.
Dans notre exemple, cela revient à vérifier si BC² = AB² + AC² ?
Etape N°3 : remplacer les éléments de la formule de Pythagore par les longueurs
On calcule le carré de nos 3 longueurs et on remplace les valeurs de notre équation.
Dans notre exemple, cela donne BC² = 10² = 100, AB² = 6² = 36 et AC² = 8² = 64.
Donc AB² + AC² = 36 + 64 = 100.
Etape N°4 : analyser les résultats et conclure sur la nature du triangle
Après les calculs de l’étape précédente, on constate que la somme AB² + AC² est bien égale à BC².
Donc, on en déduite que ABC est un triangle rectangle, dont le coté BC est l’hypoténuse et l’angle A est droit !
Nous te conseillons d’apprendre les 4 étapes du raisonnement que tu devras développer pour prouver qu’un triangle est rectangle ou non.