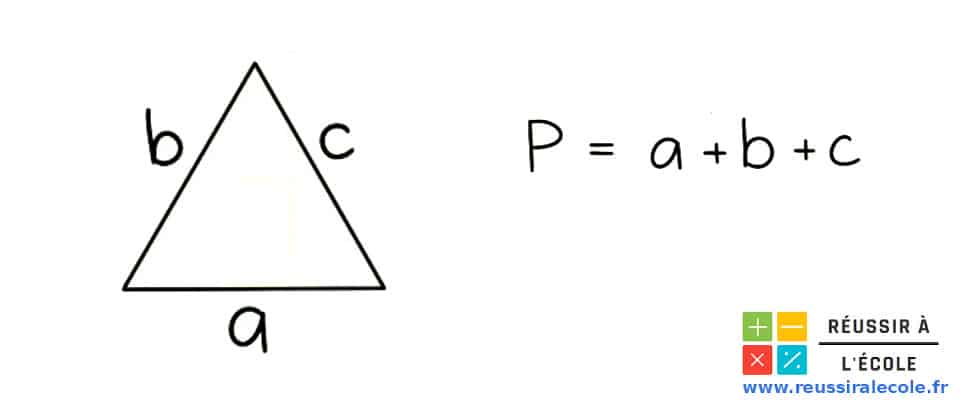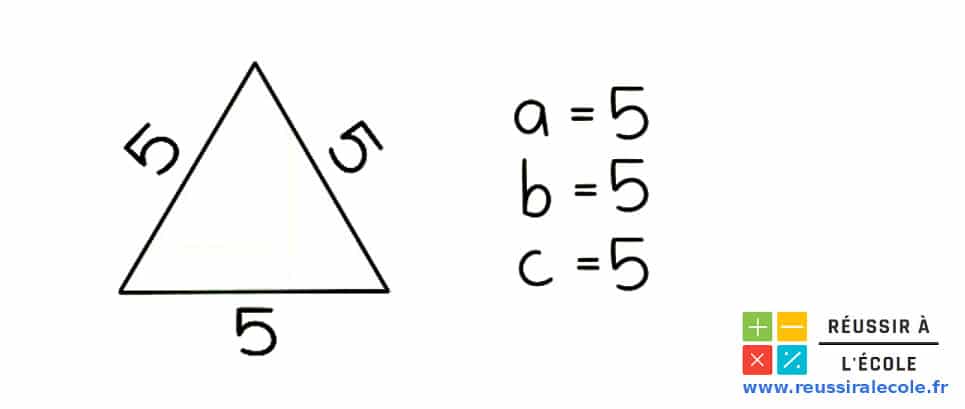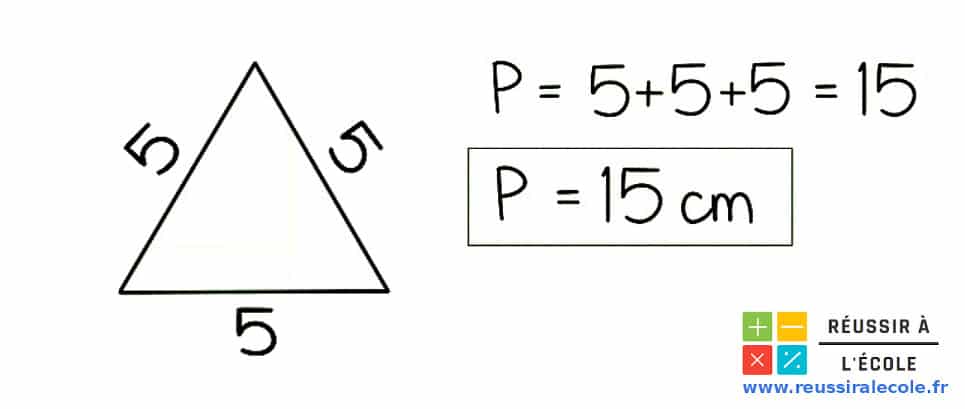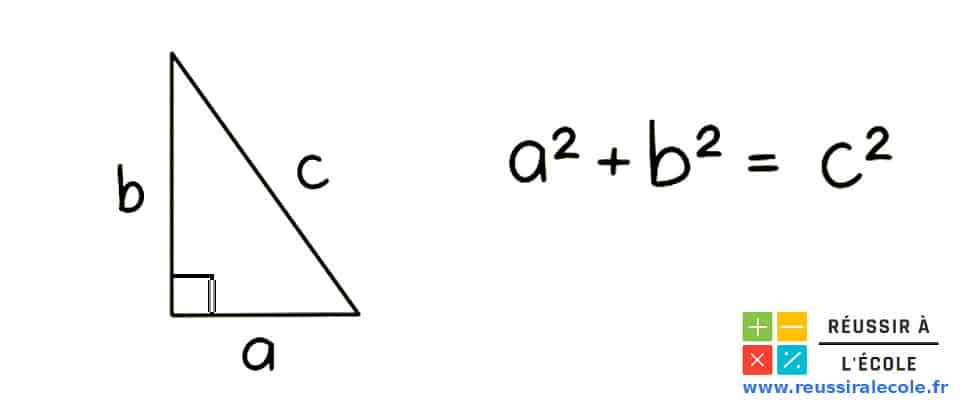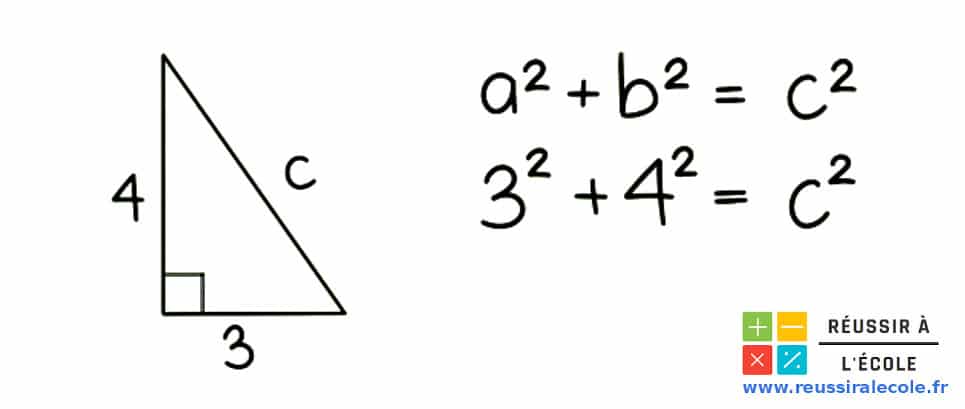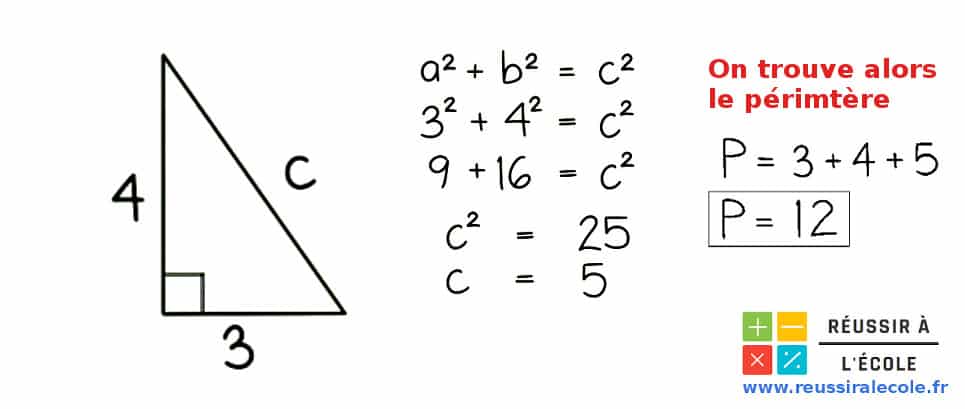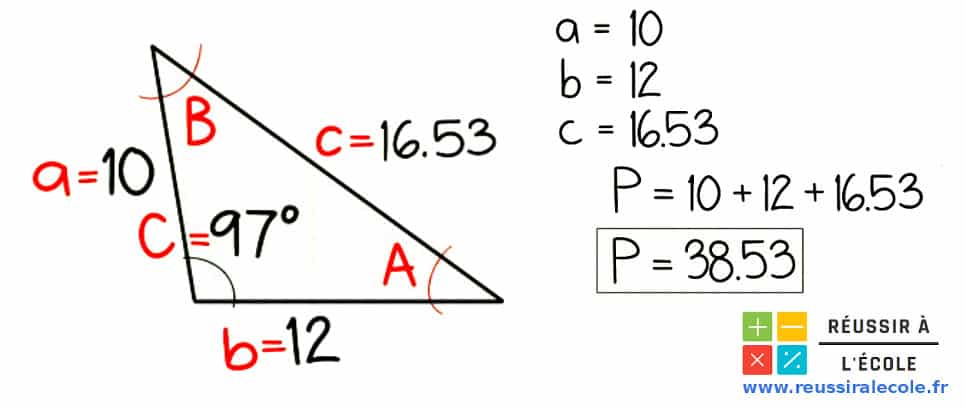Bienvenue sur notre page consacrée au perimetre du triangle.
Calculer le périmètre d un triangle, c’est tout simplement déterminer la longueur totale de son contour. D’ailleurs, la manière la plus simple de le faire est d’ajouter la longueur de chaque côté.
Mais parfois, on ignore les 3 dimensions d’un triangle…
Alors comment faire pour calculer le périmètre dans ce cas là ?
C’est ce que vous allez apprendre, en découvrant nos 3 méthodes de calcul, qui fonctionnent pour tous les types de triangle.
Comment calculer le perimetre du triangle avec la longueur des trois côtés
Tout d’abord, commençons par calculer le perimetre d un triangle en utilisant la méthode la plus simple. C’est-à-dire en ajoutant chaque côté !
Il faut noter que cette méthode est réservée aux élèves du collège en 6 ème et en 5 ème.
La formule du perimetre du triangle
Lorsque vous connaissez la longueur de tous les côtés, alors la formule de calcul est la suivante :
“ Si on appelle P, le perimetre du triangle, alors il est égal à la somme des longueurs de ses trois côtés ”.
Pour un triangle ABC, dont les longueurs sont égales à a, b et c, alors on peut écrire l’égalité suivante :
Pour connaître les dimensions a,b et c, plusieurs solutions s’offrent à vous :
- Premièrement, l’énoncé de l’exercice vous les indique
- Deuxièmement, vous pouvez les mesurer avec une règle graduée
- Troisièmement, vous pouvez déterminer les longueurs avec quelques astuces que nous vous révélerons plus bas.
Exemple de calcul du périmètre d un triangle
Dans l’exemple qui suit, la longueur des trois côtés est connue, et elle est égale à 5 cm.
Nous sommes donc en présence d’un triangle équilatéral, puisque ses trois côtés sont de même longueur. Comme la formule du perimetre d un triangle s’applique à tous les triangles sans exception, alors il suffit d’ajouter les longueurs des trois côtés pour déterminer son pourtour.
On trouve donc pour cet exemple :
Perimetre du triangle : l’erreur à ne pas commettre
A la fin de votre calcul, n’oubliez pas de préciser l’unité de mesure de la réponse. Sinon, cela n’aurait aucun sens…
D’ailleurs, il est possible de convertir le résultat en m, cm, hm, km…, mais c’est un autre sujet à aborder.
Dans notre exemple, les longueurs des côtés sont toutes indiquées en centimètres, donc le perimetre du triangle est égal à 15 cm.
Comment calculer le périmètre d un triangle rectangle avec deux côtés ?
A présent, découvrons comment calculer le perimetre du triangle rectangle si l’on ne connaît que la longueur de deux de ses côtés.
Il faut noter que cette méthode est réservée aux élèves du collège en 4 ème et en 3 ème.
Déterminer la longueur du troisième côté grâce au théorème de Pythagore
Les triangles rectangles sont souvent la hantise des élèves car on peut y appliquer le théorème de Pythagore. Mais cette fois-ci Pythagore va bien nous aider à déterminer le perimetre du triangle.
En effet, l’énoncé du théorème de Pythagore précise que :
Dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
Ainsi, on peut écrire l’égalité suivante :
Si vous connaissez la valeur de deux cotés, alors vous pouvez compléter cette équation et ainsi calculer la longueur du troisième coté.
Par exemple, si vous connaissez « a » et « b », alors il est facile de trouver « c » car cette longueur est égale à :
De cette façon, on peut obtenir chaque cote d’un triangle rectangle.
Ainsi, une fois que vous aurez trouvé la longueur manquante, alors il suffirra d’additionner les longueurs des trois cotés pour connaitre le perimetre d un triangle rectangle.
Exemple de calcul pour le perimetre du triangle rectangle
Imaginons, que l’on connaisse les deux longueurs d’un triangle rectangle (a = 3 et b = 4), mais qu’il nous manque celle de l’hypoténuse appelée « c ».
Grâce au théorème de Pythagore, on peut dire que :
Donc, pour déterminer « c » et calculer le perimetre du triangle rectangle, il faut procéder par étapes :
- Premièrement, on élève au carré les deux valeurs connues.
Donc cela donne :
9 pour « a » mis au carré et 16 pour « b » mis au carré
- Deuxièmement, on les applique à la formule de Pythagore.
On obtient alors :
- Troisièmement, on calcule la racine carré de ce résultat pour déterminer la longueur « c ». Elle est donc égale à :
- Quatrièmement, on calcule le perimetre du triangle comme suit :
Comment calculer le perimetre du triangle avec la loi des cosinus
Dans ce dernier chapitre, nous allons vous expliquer comment calculer le périmètre d un triangle quelconque si l’on connaît les longueurs de deux côtés et la valeur de l’angle qui les sépare.
Pour cela, nous allons utiliser la loi des cosinus.
D’ailleurs, il faut noter que cette méthode est réservée aux élèves du lycée.
Que dit la loi des cosinus ?
La loi des cosinus permet de déterminer le perimetre d un triangle, si l’on connaît la longueur de deux côtés et la valeur de l’angle qu’ils forment.
Cette loi est très utile, car elle fonctionne pour tous les triangles, qu’ils soient rectangles, équilatéraux, isocèles ou quelconques.
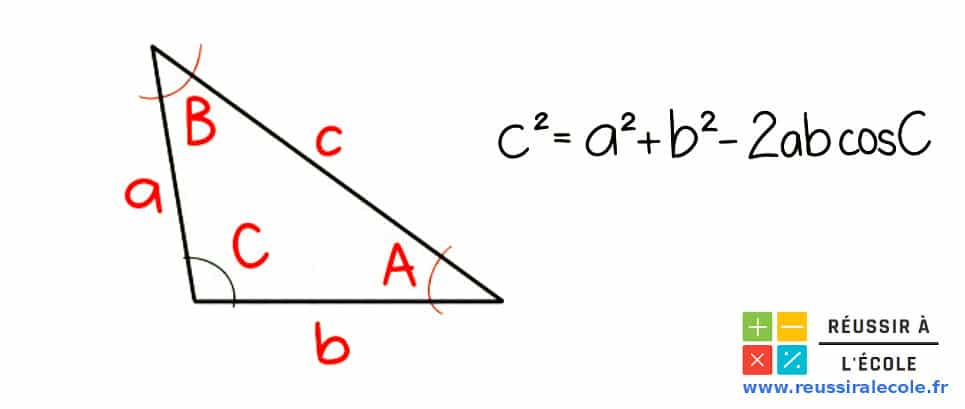
Pour tout triangle, ayant les caractéristiques suivantes :
- longueurs a, b et c
- angles A, B, C
On peut écrire l’équation suivante :
Cette égalité permet donc de déterminer la seule longueur qui est inconnue et donc de déterminer le perimetre d un triangle.
Perimetre du triangle : exemple de calcul avec la loi des cosinus
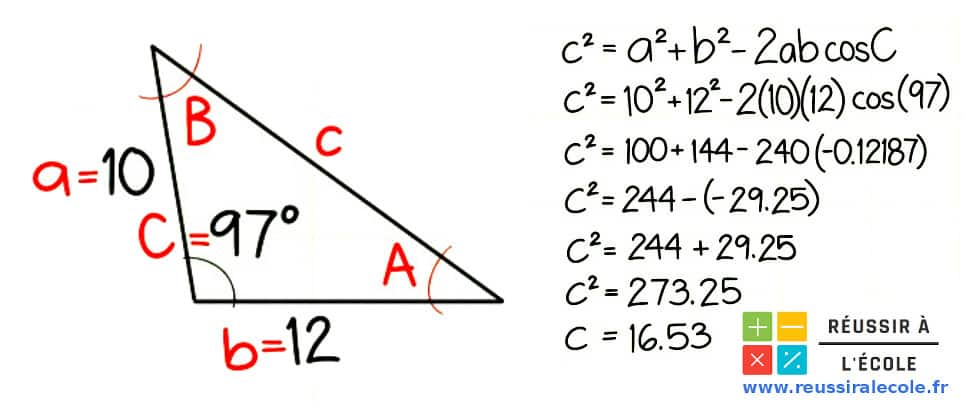
Soit un triangle ABC dont deux côtés mesurent 10 et 12 cm et dont l’angle qui les sépare est égal à 97°.
Voici donc notre méthode pour déterminer la longueur du troisième coté :
- Tout d’abord, on élève au carré les deux valeurs connues.
Donc cela donne :
- Ensuite, on calcule le cosinus de l’angle qui est :
- Puis on remplace les valeurs calculées dans l’égalité de la loi des cosinus.
Ceci donne alors :
- Alors, on détermine la longueur « c » grâce à la racine carré.
- Enfin, on calcule « P » le perimetre du triangle.
