Calculer l aire d un triangle est parfois bien plus difficile qu’il n’y paraît.
D’ailleurs, les problèmes de géométrie au collège tournent souvent autour de ce sujet.
C’est pourquoi nous avons décidé de présenter dans cet article les formules et les méthodes à utiliser pour résoudre tous les problèmes.
Nous aborderons donc différents sujets tels que :
- Comment déterminer la surface d’un triangle quelconque ou particulier (équilatéral, isocèle ou rectangle) ?
- Qu’est ce que la formule de Heron ?
- Comment utiliser le sinus et le cosinus pour calculer une surface triangulaire ?
En bref, à la fin de cet article, vous serez capables de déterminer la surface de n’importe quel triangle quelque soit ses caractéristiques.
Pour encore plus de leçons et d’exercices corrigés, n’oubliez pas de consulter notre rubrique consacrée au SOUTIEN SCOLAIRE PRIMAIRE GRATUIT.
Aire d un triangle : A quoi correspond elle et comment l’exprimer ?
En géométrie, l’aire d un triangle représente la surface qui est délimitée par les trois côtés du triangle.
L’unité de mesure utilisée est l’unité métrique mise au carré.
Généralement, on l’exprime en centimètre carré (cm²), en mètre carré (m²) ou en kilomètre carré (km²). Toutefois, on peut la convertir en hectare (ha) ou en are (a).
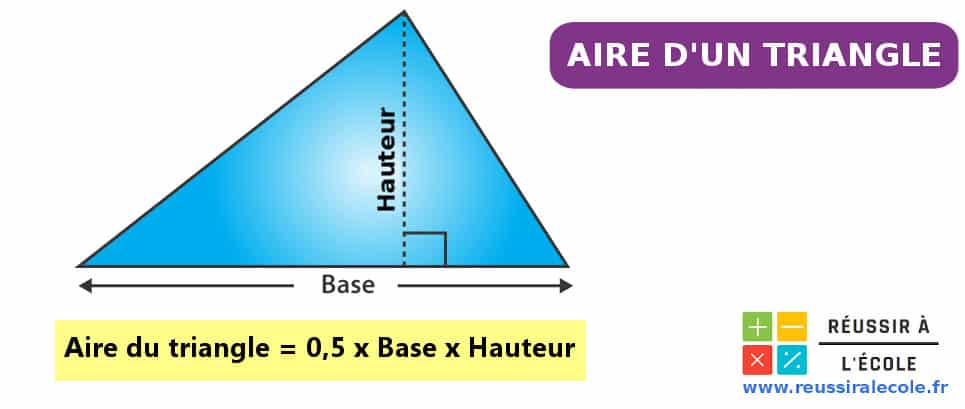
Comment calculer l aire d un triangle ?
Fondamentalement, l aire d un triangle se calcule en multipliant la base par la hauteur, et en divisant le résultat par deux.
La formule mathématique s’écrit donc de la façon suivante :
Et elle s’applique à tous les types de triangles, qu’ils soient rectangles, isocèles, équilatéraux ou quelconque.
Pour trouver l’aire d’un polygone à trois côtés grâce à cette formule, il est donc nécessaire de connaître au moins la longueur d’une base et d’une hauteur.
D’ailleurs, il est important de noter, que ces deux segments doivent obligatoirement être perpendiculaires l’un à l’autre.
Comme nous venons de le voir, il est nécessaire de connaître les longueurs d’une base et de la hauteur qui lui est associée pour calculer l’aire d’un triangle.
Mais parfois, les énoncés des exercices de mathématiques ne donnent pas directement ces deux informations. Alors il faudra faire preuve d’astuce et de méthode pour les découvrir.
Heureusement, il existe de nombreuses formules et certains théorèmes bien pratiques pour calculer l’aire d un triangle.
Voyons à présent ensemble quels sont les moyens que vous pourrez utiliser pour faire tous les exercices.
Aire d un triangle rectangle : Comment la calculer ?
Calculer l aire d un triangle rectangle n’est pas très compliqué. Mais encore faut-il savoir quelle méthode employer selon les données d’entrée du problème.
Pour vous aider à faire la plupart des exercices, nous proposons d’aborder 2 cas de figures différents pour trouver le bon résultat.
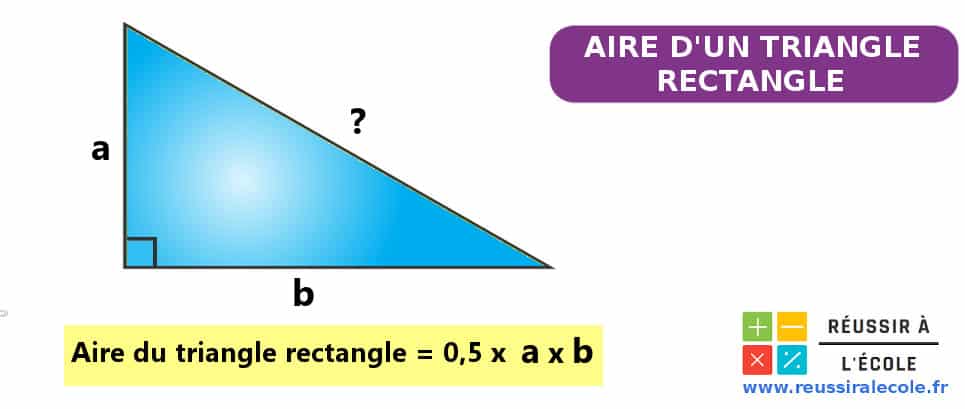
Cas N°1 : Si on connaît la longueur des côtés adjacents à l’angle droit
Quand on connait la valeur des deux cotés formant l’angle droit, alors il est très facile de trouver l’aire d’un triangle rectangle.
En effet, par définition les deux côtés adjacents de l’angle droit sont perpendiculaires.
Ils peuvent donc être indifféremment considérés comme la base et la hauteur du triangle.
Par conséquent, la mesure de leurs longueurs nous permet de calculer l aire du triangle rectangle de la façon suivante :
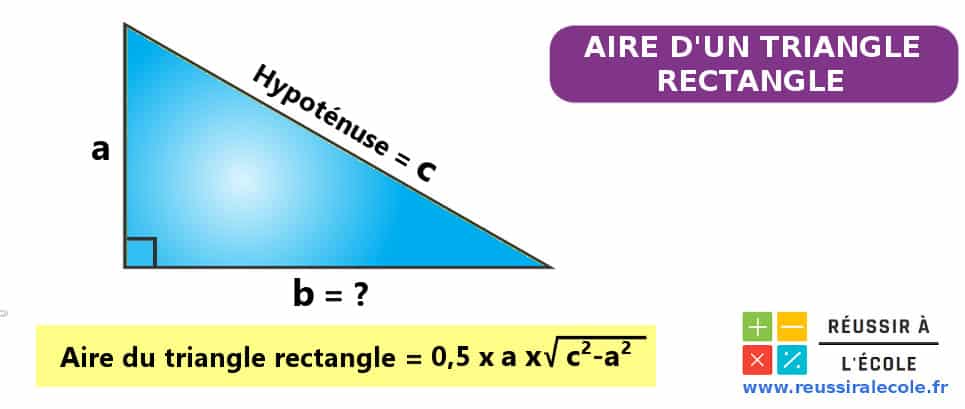
Cas N°2 : Si on connaît la longueur de l’hypoténuse et d’un autre côté
Ce cas de figure est légèrement plus compliqué sauf si l’on fait appel au théorème de Pythagore.
En effet, imaginons que l’on dispose d’un triangle où l’on connaît la longueur de l’hypoténuse “c” et d’un autre côté “a”. La longueur du troisième côté “b” étant inconnue.
On sait qu’il est possible de déterminer l’aire d un triangle si on multiplie une des bases par la hauteur qui lui est perpendiculaire. En l’occurrence, pour calculer “S” il faudrait effectuer l’opération suivante S = a x b.
Sauf que l’on connait pas la valeur de “b” pour le moment…
Mais grâce au théorème de Pythagore, on peut écrire que c² = a²+b².
Il va donc de soi que b = √(c²-a²).
Ainsi, l aire d un triangle rectangle peut se calculer en complétant la formule suivante :
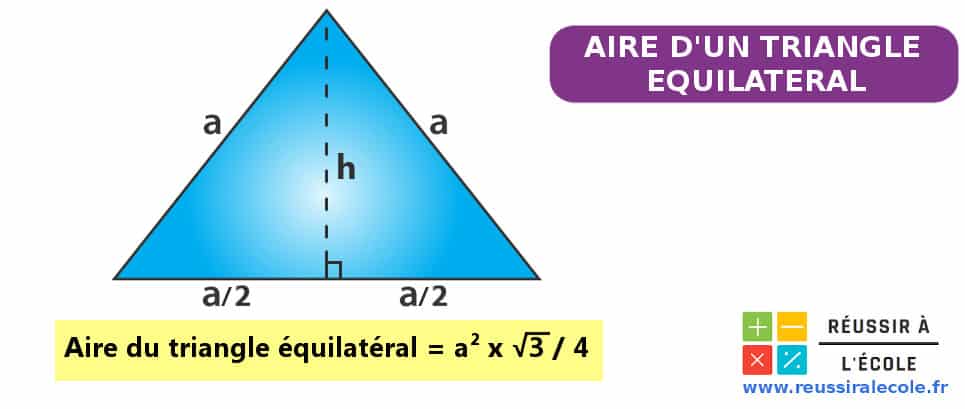
Comment calculer l’aire d’un triangle équilatéral ?
Pour calculer l aire d un triangle équilatéral, nous devons connaître la mesure d’un coté et d’une de ses hauteurs.
Si l’on dispose de la longueur des côtés du triangle, alors il nous faudra d’abord déterminer la longueur d’une hauteur pour effectuer notre calcul.
Mais comment faire pour deviner la valeur d’une des hauteurs ?
Posons les bases de notre raisonnement…
On sait qu’un triangle équilatéral possède deux caractéristiques qui lui sont propres :
- Premièrement, tous les côtés sont égaux
- Deuxièmement, les hauteurs du triangle servent également de médianes. Donc on peut affirmer que chaque hauteur tracée depuis un sommet du triangle coupe perpendiculairement la base en son milieu.
Ainsi, grâce au théorème de Pythagore, on peut écrire que :
L aire d un triangle equilateral vaut alors :
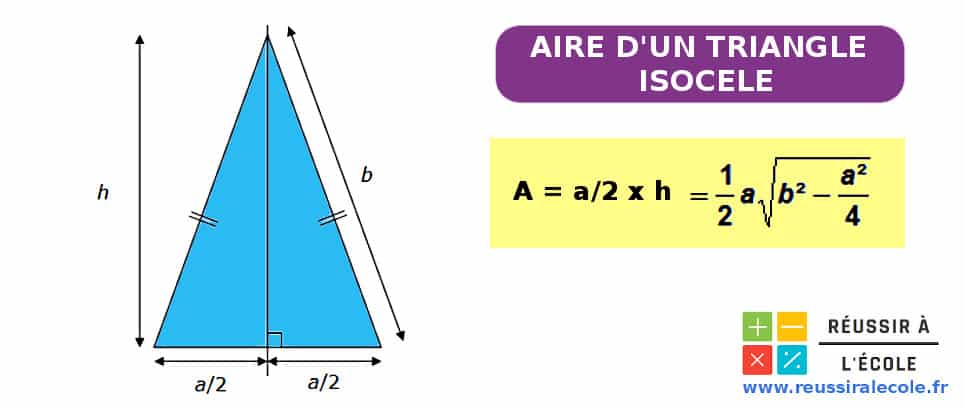
Comment calculer l’aire d’un triangle isocèle ?
Dans un triangle isocèle, on sait que deux des côtés ont la même longueur, et généralement on désigne le côté dont la longueur est différente, comme étant la base du triangle isocèle.
Par ailleurs, la médiatrice coupe la base perpendiculairement et en son milieu.
Ainsi, notre triangle isocèle peut donc se décomposer en deux triangles rectangles symétriques dont les longueurs sont h, a/2 et b comme indiqué sur notre illustration.
En appliquant le théorème de Pythagore à l’un de ces deux triangles rectangles, on obtient alors l’égalité suivante :
Celle-ci nous permet de déterminer la valeur de h en écrivant :
Alors l’aire d un triangle isocèle peut s’écrire logiquement :
Comment calculer l aire d un triangle quand on connaît la longueur de 3 côtés ?
Bonne nouvelle !
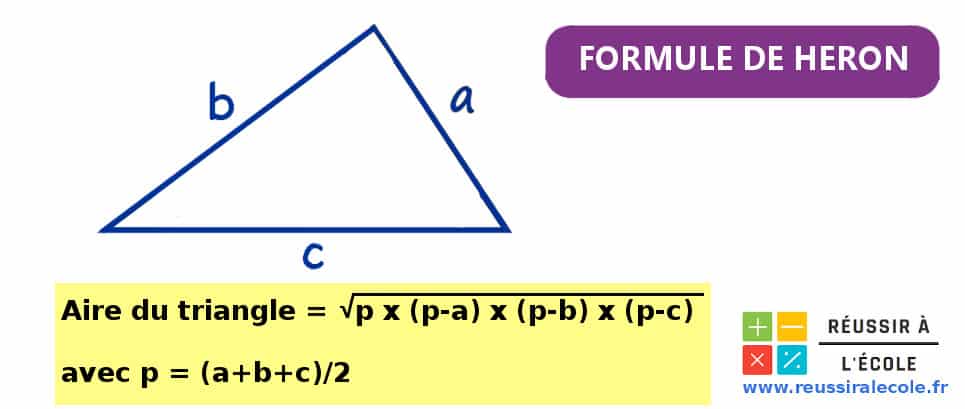
Il existe une formule pour calculer l’aire d un triangle quand on connait la longueur de ses trois côtés.
En effet, il s’agit de la formule de Heron qui s’écrit ainsi :
Pour utiliser la formule de Heron, il faut procéder en deux étapes successives.
- Premièrement, il faut calculer le demi-périmètre d un triangle. Pour cela, il suffit d’ajouter les valeurs des trois côtés et de diviser le résultat par 2.
- Deuxièmement, il faut compléter la formule de Héron avec les valeurs que l’on connaît. Cela donne alors :
où, p est le demi-périmètre du triangle et il est égal à :
Comment calculer l aire d un triangle grâce au sinus ?
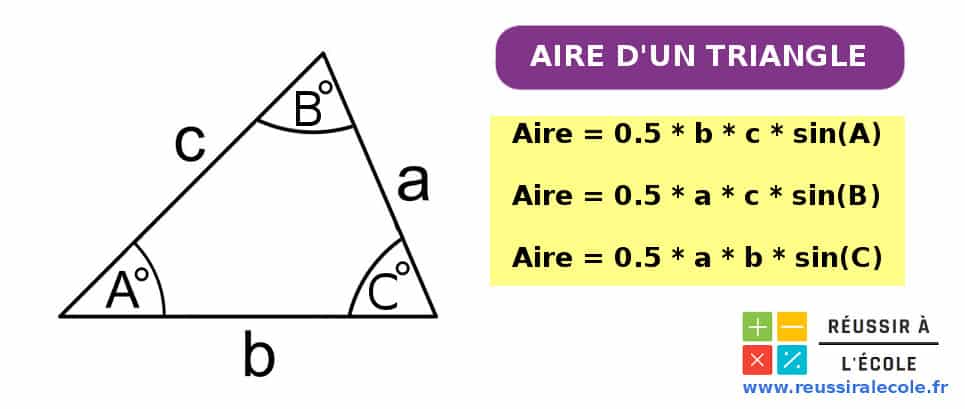
A présent, étudions le cas où l’on connaît les longueurs de deux côtés ainsi que la valeur de l’angle compris entre eux.
Dans le schéma suivant, on a donc les côtés a, b et c puis les angles A, B et C.
Pour calculer l’aire du triangle, c’est assez simple puisqu’il existe une formule facile à retenir.
Selon les côtés et les angles que nous connaissons, la formule peut être écrite de trois manières différentes :